8.5 Επικοινωνίες Πολλαπλών Θυρών

Επόμενο:8.6 Περίληψη Πάνω: Κεφάλαιο 8o: Προγράμματα περάσματος μηνυμάτων Πίσω: 8.4 Καθυστέρηση Επικοινωνίας

8.5 Επικοινωνίες Πολλαπλών Θυρών

Σε όλα τα παραδείγματα προγραμμάτων που παρουσιάστηκαν ως τώρα κάθε διεργασία είχε μόνο μια θύρα επικοινωνίας για να λαμβάνει δεδομένα από άλλες διεργασίες. Παρόλο που μια θύρα είναι γενικά επαρκής για κάθε πρόγραμμα, υπάρχουν κάποια προγράμματα στα οποία είναι πιο βολικό να υπάρχουν πολλές θύρες επικοινωνίας για κάθε διεργασία. Αυτό είναι ιδιαίτερα χρήσιμο όταν κάθε διεργασία λαμβάνει μηνύματα από αρκετές άλλες διεργασίες. Σε αυτή την περίπτωση οι επικοινωνίες πολλαπλών θυρών μπορούν να χρησιμοποιηθούν για να διακρίνουν την αφετηρία κάθε μηνύματος, έχοντας κάθε αποστολέα να γράφει σε διαφορετικές θύρες. Ένα παράδειγμα τέτοιου προγράμματος είναι η Συγχώνευση Δυο Κατευθύνσεων που παρουσιάστηκε στο 4ο κεφάλαιο. Σε αυτό το πρόγραμμα κάθε διεργασία πρέπει να έχει έναν πίνακα καναλιών για τη λήψη των τιμών που στέλνει η διεργασία-ταίρι της. Αυτό αποτελεί ένα παράδειγμα από αυτό που αποκαλούμε επικοινωνίες πολλαπλών θυρών.

8.5.1 Πολλαπλή Συλλογή

Ένα άλλο ενδιαφέρον παράδειγμα των επικοινωνιών πολλαπλών θυρών αναφέρεται στον αλγόριθμο Συλλογής και Διάδοσης για σύστημα κατανεμημένης μνήμης Υπερκύβου. Αναφέραμε στο κεφάλαιο 6 ότι μια τέτοια λειτουργία είναι ιδιαίτερα χρήσιμη στον έλεγχο σύγκλισης κατά τη διάρκεια εκτέλεσης πολλών επαναληπτικών αριθμητικών προγραμμάτων. Σε τέτοιου είδους προγράμματα μια επαναληπτική υπολογιστική διαδικασία συγκλίνει σταδιακά σε μια προσεγγιστική λύση προς την πραγματική λύση. Κατά τη διάρκεια των πρώτων επαναλήψεων συμβαίνουν μεγάλες αλλαγές στην προσεγγιστική λύση. Το μέγεθος των αλλαγών σταδιακά μειώνεται, μέχρι τελικά η αλλαγή να γίνει μικρότερη από την επιθυμητή ανοχή της λύσης. Σε αυτό το σημείο το πρόγραμμα τερματίζεται.

Στο κεφάλαιο 6 δείξαμε με ποιο τρόπο ο έλεγχος σύγκλισης μπορεί να πραγματοποιηθεί παράλληλα έχοντας κάθε διεργασία να εφαρμόζει τον έλεγχο τοπικά και να παράγει μια λογική τιμή. Στην συνέχεια οι λογικές τιμές όλων των διεργασιών ομαδοποιούνται για να καθορίσουν αν επιτεύχθηκε η γενική σύγκλιση και για να διαδώσουν το αποτέλεσμα σε όλες τις διεργασίες. Για την τοπολογία του Υπερκύβου η τεχνική του Τουρνουά που παρουσιάστηκε στο κεφάλαιο 6 είναι ιδιαίτερα χρήσιμη όλες οι απευθείας επικοινωνίες λαμβάνουν χώρα μεταξύ διεργασιών των οποίων οι δυαδικοί αριθμοί διαφέρουν μόνο κατά ένα bit. Έτσι, αν αυτός ο αλγόριθμος Τουρνουά εκτελείται στον Υπερκύβο κάθε μήνυμα χρειάζεται να διασχίσει μόνο έναν απλό σύνδεσμο επικοινωνίας για να φτάσει τον προορισμό του.

Σε αυτό τον αλγόριθμο Τουρνουά όλες οι λογικές τιμές από όλες τις διεργασίες σταδιακά συγκλίνουν μέσα από ένα δυαδικό δένδρο στη διεργασία 0, η οποία είναι η ρίζα του δένδρου. Η διεργασία 0 διαδίδει κάθετα στο δυαδικό δένδρο την τελική ομαδοποιημένη τιμή σε όλες τις υπόλοιπες διεργασίες που συντελούν τη δομή του δένδρου (δες σχήματα 6.8 και 6.9). Για έναν Υπερκύβο με n επεξεργαστές και βασική καθυστέρηση επικοινωνίας D το σύνολο της επιβάρυνσης του χρόνου επικοινωνίας που απαιτείται για αυτόν τον αλγόριθμο είναι 2Dlogn. Ο πολλαπλασιαστής 2 σε αυτό τον τύπο προκύπτει από το γεγονός ότι το δυαδικό δένδρο διασχίζεται δύο φορές. Χρησιμοποιώντας ένα λίγο διαφορετικό αλγόριθμο είναι δυνατή η διάσχιση του δένδρου μια φορά και συνεπώς η μείωση της επιβάρυνσης επικοινωνίας κατά το συντελεστή 2.

Σε αυτό το νέο αλγόριθμο, που ονομάζεται Πολλαπλή Συλλογή, δημιουργούνται πολλά δυαδικά δένδρα ταυτόχρονα, έτσι ώστε κάθε επεξεργαστής να ανατίθεται στην ρίζα κάθε τέτοιου δένδρου. Με αυτό τον τρόπο η διάσχιση του δένδρου συμβαίνει μόνο μια φορά. Με αυτό το νέο αλγόριθμο ομαδοποίησης κάθε επεξεργαστής διαλέγει το ταίρι με το οποίο θα επικοινωνήσει σε κάθε στάδιο, εξετάζοντας τα bits του δικού του αριθμού. Για ένα Υπερκύβο με διάσταση d κάθε αριθμός επεξεργαστή έχει d bits. Αυτά τα bits μπορούν να αριθμηθούν από δεξιά προς τα αριστερά, από το 1 ως το d. Ο αλγόριθμος ομαδοποίησης έχει d βήματα. Στο βήμα i, κάθε επεξεργαστής καθορίζει το ταίρι με το οποίο θα επικοινωνεί αντιστρέφοντας το i-οστό bit του δικού του αριθμού επεξεργαστή. Κάθε επεξεργαστής διατηρεί τη δική του εσωτερική Boolean τιμή. Κατά τη διάρκεια του βήματος i στέλνει την λογική τιμή του στο ταίρι του και λαμβάνει ένα αντίστοιχο αντίγραφο από το ταίρι του με τη δική του λογική τιμή. Στη συνέχεια η λογική τιμή που έχει λάβει συγχωνεύεται με τη δική του εσωτερική τιμή χρησιμοποιώντας μια λειτουργία AND.

Παρακάτω παρουσιάζουμε μια υψηλού επιπέδου περιγραφή του αλγορίθμου της Πολλαπλής Ομαδοποίησης. Κάθε επεξεργαστής θα εκτελεί τον παρακάτω κώδικα:

FOR i:=1 to d DO


    BEGIN


        Compute “partner” by reversing ith bit of my number;


        Send “myboolean” to partner;


        Receive “hisboolean” from partner;


        myboolean:= myboolean AND hisboolean;


    END;


final result is in “myboolean”;

Για έναν Υπερκύβο με διάσταση 3 το σχήμα 8.9 δείχνει τη συνολική δομή του αλγορίθμου της Πολλαπλής Συλλογής. Κάθε έντονη κάθετη γραμμή αναπαριστά έναν από τους εννιά επεξεργαστές. Τα διαγώνια τόξα δείχνουν την επικοινωνία που συμβαίνει σε κάθε βήμα του αλγόριθμου. Παρατηρείστε ότι τα ζεύγη επικοινωνίας σε κάθε διαδοχικό βήμα απέχουν τη διπλάσια απόσταση από το προηγούμενο βήμα. Αυτό συμβαίνει γιατί για να καθοριστεί το κάθε ταίρι τα bits του αριθμού του κάθε επεξεργαστή εξετάζονται από τα δεξιά προς τα αριστερά. Στην ουσία αυτό το πρότυπο είναι το ίδιο με αυτό που χρησιμοποιήθηκε στο δίκτυο διασύνδεσης της πεταλούδας, που παρουσιάστηκε στο σχήμα 3.7. Αυτό το πρότυπο της πεταλούδας είναι χρήσιμο σε πολλούς διαφορετικούς αλγόριθμους, ειδικά όταν έχουν σχέση με τοπολογίες Υπερκύβου.

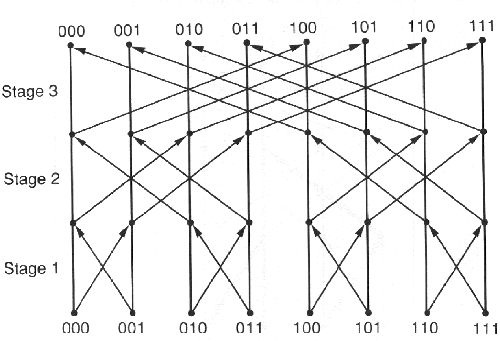
ΣΧΗΜΑ 8.9 Συλλογή σε υπερκύβο

Με μια προσεκτική ματιά στο σχήμα 8.9 βλέπουμε ότι κάθε επεξεργαστής βρίσκεται στη ρίζα του δικού του δυαδικού δένδρου με όλους τους άλλους επεξεργαστές στα φύλλα αυτού του δένδρου. Αυτό παρουσιάζεται με ακρίβεια στο σχήμα 8.10. Το δυαδικό δένδρο που έχει ρίζα το 010 προσδιορίζεται από τις πιο έντονες σκούρες γραμμές στο πρότυπο της πεταλούδας. Σε κάθε κόμβο αυτής της δυαδικής δομής ο αλγόριθμος πραγματοποιεί μια λογική λειτουργία AND. Συνεπώς, ο επεξεργαστής 010 θα λάβει τα συνδυασμένα λογικά AND όλων των αρχικών Boolean τιμών όλων των επεξεργαστών. Εφόσον κάθε επεξεργαστής είναι η κορυφή του δικού του δυαδικού δένδρου θα λάβει τα ίδια συνδυασμένα λογικά AND όλων των αρχικών Boolean τιμών. Υλοποιώντας όλα αυτά τα δυαδικά δένδρα παράλληλα μειώνεται η αναγκαιότητα της διπλής διάσχισης του δένδρου, όπως συμβαίνει στον αλγόριθμο Τουρνουά στο κεφάλαιο 6. Για έναν Υπερκύβο με n επεξεργαστές και βασική καθυστέρηση επικοινωνίας D αυτός ο αλγόριθμος Πολλαπλής Συλλογής έχει Dlogn επιβάρυνση επικοινωνίας, με την προϋπόθεση ότι κάθε φυσικός σύνδεσμος επικοινωνίας μπορεί να μεταδώσει μηνύματα και προς τις δύο κατευθύνσεις ταυτόχρονα.

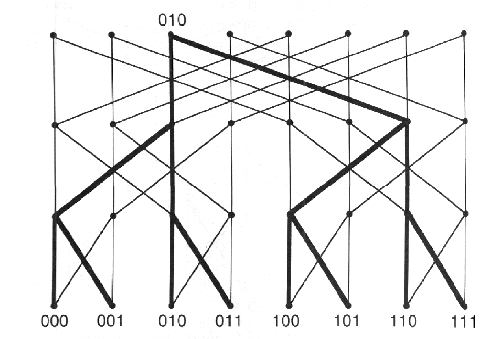
ΣΧΗΜΑ 8.10 Δυαδικό δένδρο σε πρότυπο πεταλούδας

Για να εφαρμόσουμε τον αλγόριθμο Πολλαπλής Συλλογής με Multi-Pascal πρέπει κάθε διεργασία να έχει ξεχωριστές θύρες επικοινωνίας για κάθε ταίρι της. Για να δουλέψει ο αλγόριθμος σωστά είναι απαραίτητο τα δεδομένα της επικοινωνίας του από κάθε ταίρι να επεξεργάζονται με την κατάλληλη ακολουθία. Μια από τις ασκήσεις στο τέλος του κεφαλαίου ασχολείται με τη φύση των λαθών που προκύπτουν αν η επεξεργασία της επικοινωνίας δεν γίνεται με την κατάλληλη σειρά. Εφόσον όλα τα ταίρια μπορούν να εκτελούνται σε διαφορετικές ταχύτητες οι επικοινωνίες μπορούν στην πραγματικότητα να εκτελούνται με τυχαία σειρά. Συνεπώς, κάθε διεργασία απαιτεί μια ξεχωριστή θύρα επικοινωνίας για να επικοινωνεί με κάθε ταίρι της. Αυτό στην Multi-Pascal επιτυγχάνεται με ένα διδιάστατο πίνακα καναλιών:

inchan: ARRAY [0..n, 1..d] OF CHANNEL OF BOOLEAN;

Ο πρώτος δείκτης αφορά όλες τις διεργασίες και ο δεύτερος όλα τα ταίρια επικοινωνίας κάθε διεργασίας. Όταν κάθε διεργασία i δημιουργείται λαμβάνει τον inchan[i] σαν τον πίνακα των θυρών επικοινωνίας της. Κατά τη διάρκεια του βήματος k του αλγόριθμου η διεργασία i θα λάβει μηνύματα από τη θύρα inchan[i,k]. Η χρήση ενός πίνακα θυρών σε κάθε διεργασία επιτρέπει την ακολουθιακή θεώρηση των επικοινωνιών. Ο συνολικός κώδικας σε Multi-Pascal φαίνεται στο σχήμα 8.11. Η συνάρτηση “Aggregate” λαμβάνει μια Boolean τιμή την mydone από κάθε διεργασία και στη συνέχεια επιστρέφει την τελική ομαδοποίηση των Boolean τιμών ως το αποτέλεσμα της.

PROGRAM MultipleAggregate;


ARCHITECTURE HYPERCUBE(6); (*Τοπολογία Υπερκύβου διάστασης 6*)


CONST d=6; (*Διάσταση του Υπερκύβου*)


      n=63;


VAR inchan: ARRAY [0..n, 1..d] OF CHANNEL OF BOOLEAN; (*Θύρες επικοινωνίας*)


    i: INTEGER;


FUNCTION Aggregate(mydone: BOOLEAN): BOOLEAN;


VAR mynum, partner, bitvalue, stage: INTEGER;


    hisdone: BOOLEAN;


BEGIN


    mynum:=%SELF; (*Λήψη του αριθμού επεξεργαστή*)


    bitvalue:= 1;


    FOR stage:= 1 TO d DO


    BEGIN


        IF mynum DIV bitvalue MOD 2 = 0 (*Υπολογισμός του ζεύγους*)


            THEN partner:= mynum+bitvalue


        ELSE partner:= mynum-bitvalue;


        inchan[partner, stage]:= mydone; (*Αποστολή του mydone στο ταίρι*)


        hisdone:= inchan[mynum, stage]; (*Λήψη του hisdone από το ταίρι*)


        mydone:= mydone AND hisdone;


        bitvalue:= 2*bitvalue (*Μετατόπιση προς την επόμενη θέση bit*)


       END;


    Aggregate:= mydone;


END;


PROCEDURE Process(i: INTEGER);


VAR mydone, done: BOOLEAN;


BEGIN


REPEAT
    .... (*Πραγματοποίηση επανάληψης και υπολογισμός της mydone*)


    done:= Aggregate(mydone);


UNTIL done;


END;


BEGIN (*Κυρίως πρόγραμμα*)


    ....


    FORALL i:= 0 TO n DO


        (@i PORT inchan[i]) Process(i); (*Δημιουργία των διεργασιών*)


END.

ΣΧΗΜΑ 8.11 Συνάρτηση Πολλαπλής Συλλογής

8.5.2 Πολλαπλή Διάδοση

Ο αλγόριθμος Πολλαπλής Συλλογής μπορεί εύκολα να μετατραπεί σε αυτό που ονομάζουμε αλγόριθμο Πολλαπλής Διάδοσης. Σε κάθε συνηθισμένη διάδοση μια διεργασία διαδίδει ένα αντίγραφο των δεδομένων της σε κάθε άλλη διεργασία. Σε μια πολλαπλή διάδοση κάθε διεργασία πραγματοποιεί μια διάδοση την ίδια χρονική στιγμή. Αν έχουμε n διεργασίες μια πολλαπλή διάδοση θα έχει ως αποτέλεσμα κάθε διεργασία να λάβει n δεδομένα. Ο αλγόριθμος Πολλαπλής Συλλογής μπορεί να τροποποιηθεί σε Πολλαπλής Διάδοσης απλά αν αντικαταστήσουμε τη λογική λειτουργία AND με μια λειτουργία “συνένωσης λίστας”. Αυτό σημαίνει ότι η παράμετρος mydone κάθε διεργασίας θα αντικατασταθεί από μια λίστα με όλες τις λαμβανόμενες τιμές mylist. Όταν η mylist αποστέλλεται στη διεργασία ταίρι τότε στέλνεται όλη η λίστα. Όταν μια λίστα λαμβάνεται από τη διεργασία ταίρι, τότε όλη η λίστα απλά συνενώνεται με την εσωτερική mylist. Όταν ο αλγόριθμος τελειώνει η εσωτερική mylist κάθε διεργασίας θα περιέχει ένα αντίγραφο των προτύπων τιμών από τις n διεργασίες.

Ο κώδικας της Multi-Pascal φαίνεται στο σχήμα 8.12. Η διαδικασία “Broadcast” λαμβάνει μόνο την ακέραια τιμή myvalue από κάθε διεργασία και επιστρέφει μια λίστα n ακεραίων τιμών στην παράμετρο πίνακα mylist. Είναι ενδιαφέρουσα η ανάλυση του μεγέθους του mylist σε κάθε βήμα της διάδοσης. Κατά τη διάρκεια κάθε βήματος κάθε διεργασία λαμβάνει όλη τη λίστα από το ταίρι της και την συνενώνει με την mylist. Έτσι, το μέγεθος του mylist θα διπλασιαστεί κατά τη διάρκεια κάθε βήματος. Ο αριθμός των λειτουργιών επικοινωνίας που πραγματοποιούνται από μια διεργασία κατά τη διάρκεια κάθε βήματος είναι ίσος με το διπλάσιο μέγεθος της λίστας, εφόσον μια λίστα λαμβάνεται και αποστέλλεται κατά τη διάρκεια κάθε βήματος. Για έναν Υπερκύβο με n επεξεργαστές και διάσταση d ο συνολικός αριθμός των λειτουργιών επικοινωνίας που πραγματοποιούνται κατά τη διάρκεια των d βημάτων της διάδοσης είναι :

2¹+ 2² + 2³ + ... + 2^d= 2 ( 2^d - 1 ) = 2 ( n - 1 )

Εφόσον οι λειτουργίες επικοινωνίας είναι αυτές που σπαταλούν τον περισσότερο χρόνο όλος ο αλγόριθμος της Πολλαπλής Διάδοσης θα έχει O(n) χρόνο εκτέλεσης. Ο χρόνος αυτός έρχεται σε αντίθεση με τον αντίστοιχο χρόνο του αλγορίθμου Πολλαπλής Συλλογής, που είναι O(logn). Ακόμα και ο αριθμός των βημάτων στην Πολλαπλή Διάδοση, logn, είναι ο διπλάσιος από το μέγεθος της λίστας στο τέλος του κάθε βήματος με χρόνο εκτέλεσης O(n).

Η σύγκριση αυτού του αλγορίθμου με κάποιον άλλο αλγόριθμο Πολλαπλής Διάδοσης, στον οποίο κάθε διεργασία απλά στέλνει ένα αντίγραφο της εσωτερικής της τιμής απευθείας σε κάθε άλλη διεργασία, δεν είναι έντιμη. Αυτό μπορεί να γίνει με ένα FOR βρόχο σε κάθε διεργασία που επαναλαμβάνεται σε όλες τις n διεργασίες, στέλνοντας σε καθεμία από αυτές ένα αντίγραφο της τιμής. Αυτό παρουσιάζεται στη διαδικασία Broadcast στο σχήμα 8.13. Ο αριθμός των λειτουργιών επικοινωνίας σε αυτή την πιο απλοϊκή προσέγγιση είναι 2n, δηλαδή ο ίδιος με του προηγούμενου αλγορίθμου. Συνεπώς, προκύπτει η ίδια επιβάρυνση λογισμικού. Επίσης, ο αλγόριθμος δρομολόγησης αυτόματου μηνύματος Υπερκύβου εξασφαλίζει ότι όλα τα μηνύματα θα πάρουν το μονοπάτι με τη μικρότερη απόσταση από τον προορισμό τους. Όμως, αυτή η μέθοδος έχει πρόβλημα σχετικά με την πιθανότητα σοβαρής συμφόρησης στο δίκτυο επικοινωνίας που μπορεί να προκαλέσει σοβαρή μείωση της απόδοσης. Στη συνέχεια αυτή η νέα μέθοδος πολλαπλής διάδοσης θα ονομάζεται “Άμεση” μέθοδος και η προηγούμενη μέθοδος θα ονομάζεται μέθοδος της “Πεταλούδας”.

PROGRAM MultipleBroadcast;


ARCHITECTURE HYPERCUBE(6); (*Τοπολογία Υπερκύβου με διάσταση 6*)


CONST d= 6;


    n= 63;


TYPE listtype= ARRAY [0..n] OF INTEGER;


VAR inchan: ARRAY [0..n, 1..d] OF CHANNEL OF INTEGER; (*Θύρες επικοινωνίας*)


    i: INTEGER;


PROCEDURE Broadcast(myvalue: INTEGER; VAR mylist: listtype);


VAR mynum, bitvalue, stage, j: INTEGER;


    hisdone: BOOLEAN;


BEGIN


    mynum:= %SELF;


    mylist[0]:= myvalue;


    bitvalue:= 1;


    FOR stage:= 1 TO d DO


    BEGIN


        IF mynum DIV bitvalue MOD 2 = 0 (*Υπολογισμός του ταιριού*)


            THEN partner:= mynum+bitvalue


        ELSE partner:= mynum-bitvalue;


        FOR j:= 0 TO bitvalue-1 DO (*Αποστολή του mylist στο ταίρι*)


                inchan[partner,stage]:= mylist[j];


        FOR j:= bitvalue TO 2*bitvalue-1 DO


            mylist[j]:=inchan[mynum,stage](*Λήψη της λίστας από το ταίρι*)


        bitvalue:= 2*bitvalue; (*Μετατόπιση στην επόμενη θέση bit*)


    END;


END;


PROCEDURE Process(i: INTEGER);


VAR values: listtype;


myvalue: INTEGER;


BEGIN


    ...


    Broadcast(myvalue, values); (*Αποστολή της myvalue σε όλες τις διεργασίες*)


    (*Λήψη στον πίνακα values*)


END;


BEGIN (*Κυρίως πρόγραμμα*)


    ...


    FORALL i:= 0 TO n DO


        (@i PORT inchan[i]) Process(i); (*Δημιουργία των διεργασιών*)


END.

ΣΧΗΜΑ 8.12 Πολλαπλή Διάδοση σε Υπερκύβο

PROGRAM DirectBroadcast;


ARCHITECTURE HYPERCUBE(6);


CONST d= 6;


    n= 63;


TYPE listtype= ARRAY [0..n] OF INTEGER;


VAR inchan: ARRAY [0..n, 1..d] OF CHANNEL OF INTEGER;


    ...


PROCEDURE Broadcast(myvalue: INTEGER; VAR values:listtype);


VAR mynum, bitvalue, stage, i: INTEGER;


    hisdone: BOOLEAN;


BEGIN


    mynum:= %SELF;


    FOR i:= 0 TO n DO (*Αποστολή ενός αντιγραφου της myvalue σε όλες τις διεργασίες*)


        inchan[i]:= myvalue;


    FOR i:= 0 TO n DO (*Λήψη των τιμών που έχουν στείλει οι άλλες διεργασίες*)


        values[i]:= inchan[mynum];


END;


...

ΣΧΗΜΑ 8.13 Πολλαπλή Διάδοση με συμφόρηση

Στην Άμεση μέθοδο καθεμία από τις n διεργασίες στέλνει n μηνύματα στο δίκτυο επικοινωνίας. Αυτά τα n² μηνύματα μπορούν να προκαλέσουν σημαντική συμφόρηση. Όμως, η μέθοδος της Πεταλούδας είναι έτσι σχεδιασμένη, ώστε να ελαχιστοποιεί την πιθανότητα συμφόρησης. Σε κάθε στάδιο κάθε επεξεργαστής επικοινωνεί με το ταίρι του με τον απευθείας σύνδεσμο επικοινωνίας που τους συνδέει. Συνεπώς δεν μπορεί να συμβεί καμιά παρεμβολή μεταξύ αυτών των μηνυμάτων. Χρησιμοποιώντας τη Multi-Pascal συγκρίναμε την απόδοση αυτών των δύο αλγορίθμων Πολλαπλής Διάδοσης για διάφορες τιμές της βασικής καθυστέρησης επικοινωνίας, από 0 ως 100, σε τοπολογία Υπερκύβου με n=32 επεξεργαστές. Τα αποτελέσματα φαίνονται στο γράφημα του σχήματος 8.14. Εφόσον η Άμεση μέθοδος έχει μια ελαφρώς χαμηλότερη επιβάρυνση λογισμικού, παρουσιάζει ανώτερη απόδοση για μικρότερες τιμές της βασικής καθυστέρησης. Όμως, καθώς η βασική καθυστέρηση αυξάνεται η συμφόρηση προκαλεί την ραγδαία αύξηση του χρόνου εκτέλεσης στην Άμεση μέθοδο. Η αύξηση στην βασική καθυστέρηση προκαλεί επίσης αύξηση του χρόνου και στην μέθοδο της Πεταλούδας, αλλά πιο βαθμιαία.

Το σημείο διασταύρωσης των δύο καμπυλών στο σχήμα 8.14 είναι η βασική καθυστέρηση 22. Συνεπώς, για καθυστέρηση μεγαλύτερη από 22, η μέθοδος της Πεταλούδας έχει ανώτερη απόδοση. Αυτό αναφορικά με το σύστημα κατανεμημένης μνήμης Υπερκύβου με n=32 επεξεργαστές. Είναι διδακτικό να δούμε πως αυτό το σημείο τομής αλλάζει για διαφορετικές τιμές του n. Αυτό παρουσιάζεται στο σχήμα 8.15 για n=4, 8, 16, 32, 64. Η ενιαία γραμμή στο γράφημα συνδέει τα σημεία τομής για τις διάφορες τιμές του n. Στα δεξιά αυτής της γραμμής είναι η περιοχή στην οποία η μέθοδος Πολλαπλής Διάδοσης της Πεταλούδας παρουσιάζει ανώτερη απόδοση, συγκρινόμενη με την Άμεση μέθοδο Πολλαπλής Διάδοσης. Στα αριστερά της γραμμής η Άμεση μέθοδος έχει ανώτερη απόδοση. Το σχήμα αυτού του γραφήματος δείχνει ότι για μικρότερο αριθμό επεξεργαστών η καθυστέρηση επικοινωνίας πρέπει να αυξηθεί σε μια υψηλή τιμή πριν η συμφόρηση στην Άμεση μέθοδο γίνει πρόβλημα.

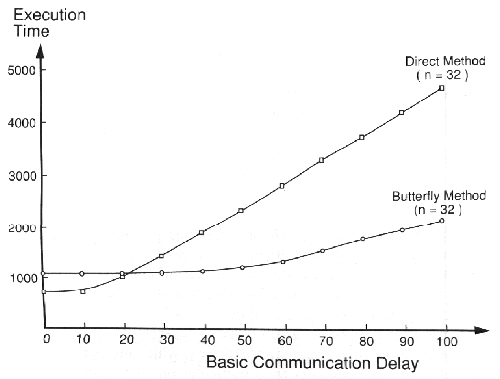
ΣΧΗΜΑ 8.14 Σύγκριση μεθόδων πολλαπλών μεταδόσεων

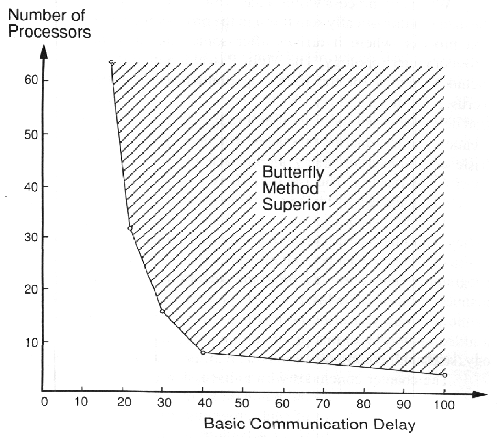
ΣΧΗΜΑ 8.15 Περιοχή ανώτερης απόδοσης της Πολλαπλής Διάδοσης Πεταλούδας