7.3 Διάδοση και Συλλογή

Επόμενο:7.4 Απεικονίσεις πάνω στον Υπερκύβο Πάνω: Κεφάλαιο 7o : Αρχιτεκτονική συστημάτων κατανεμημένης μνήμης Πίσω: 7.2 Τοπολογίες Συστημάτων Κατανεμημένης Μνήμης

7.3 Διάδοση και Συλλογή

Για να κατανοήσουμε περισσότερο τη δομή και τη σχέση μεταξύ των διαφόρων τοπολογιών παράλληλων συστημάτων κατανεμημένης μνήμης θα ήταν χρήσιμο να αναλύσουμε την εφαρμογή δύο σημαντικών λειτουργιών που συμβαίνουν συχνά σε μια μεγάλη ποικιλία παράλληλων αλγορίθμων: τη διάδοση και τη συλλογή. Αυτές οι λειτουργίες αναπτύχθηκαν ήδη στο κεφάλαιο 6 με αναφορά σε μια από τις μεγαλύτερες τεχνικές οργάνωσης των παράλληλων προγραμμάτων: Υπολογισμός, Συλλογή και Διάδοση. Οι επαναληπτικοί αριθμητικοί αλγόριθμοι, όπως είναι η μέθοδος Jacobi, συνήθως απαιτούν ένα περιοδικό έλεγχο σύγκλισης για να καθορίσουν αν το πρόγραμμα πρέπει να σταματήσει ή όχι. Αυτή η διαδικασία περιλαμβάνει συλλογή των τοπικών ελέγχων σύγκλισης από κάθε επεξεργαστή και κατόπιν διάδοση του τελικού αποτελέσματος πίσω σε κάθε επεξεργαστή.

Για τους σκοπούς αυτού του κεφαλαίου, θα ορίσουμε τη διάδοση ως τη λειτουργία διανομής ενός αντιγράφου δεδομένων από τον επεξεργαστή 0 σε όλους τους επεξεργαστές σε σύστημα κατανεμημένης μνήμης. Η συλλογή ορίζεται ως η ομαδοποίηση δεδομένων από κάθε επεξεργαστή και ο συνδυασμός τους σε ένα μόνο αντικείμενο δεδομένων, με μια σταδιακή εφαρμογή μιας λειτουργίας που συνδυάζει ένα ζευγάρι δεδομένων σε ένα μόνο δεδομένο. Υποθέτουμε ότι η λειτουργία συνδυασμού έχει την προσεταιριστική ιδιότητα, που σημαίνει ότι το τελικό αποτέλεσμα είναι ανεξάρτητο από τη σειρά με την οποία συνδυάζονται τα δεδομένα. Με παρόμοιο τρόπο ο έλεγχος σύγκλισης στο πρόγραμμα Jacobi γινόταν εφαρμόζοντας την λειτουργία AND στην Boolean μεταβλητή mydone που παραγόταν από κάθε διεργασία. Το αποτέλεσμα ήταν μια γενική μεταβλητή Boolean που δήλωνε αν έπρεπε το πρόγραμμα να τερματιστεί.

Είναι σημαντικό να αναφέρουμε ότι η διάδοση και η συλλογή είναι περίπου όμοιες λειτουργίες με τη διαφορά ότι λειτουργούν προς την αντίθετη κατεύθυνση. Η διάδοση διαδίδει μια μόνο τιμή σε όλους τους επεξεργαστές και η συλλογή συλλέγει μια τιμή από κάθε επεξεργαστή και συνδυάζει όλες τις τιμές σε μια. Η διάδοση κινείται από τον επεξεργαστή 0 προς όλους τους υπόλοιπους, ενώ η συλλογή κινείται από όλους τους επεξεργαστές προς τον 0. Σε ένα παράλληλο σύστημα κατανεμημένης μνήμης η συνολική υπολογιστική μέθοδος και ο χρόνος που αυτή καταλαμβάνει είναι τα ίδια και για τη συλλογή και για τη διάδοση, με τη διαφορά ότι η ροή των δεδομένων είναι προς αντίθετες κατευθύνσεις στις δυο λειτουργίες. Στην διάδοση η ροή των δεδομένων γίνεται από τον επεξεργαστή 0 προς τους γειτονικούς επεξεργαστές από όπου αντιγράφονται και μεταδίδονται στους επόμενους γείτονες μέχρι όλοι οι επεξεργαστές να παραλάβουν ένα αντίγραφο. Η συλλογή είναι μια διάδοση που λειτουργεί αντίστροφα στο χρόνο και τις τιμές να ρέουν προς τον επεξεργαστή 0 αντί να απομακρύνονται από αυτόν.

Η όλη λειτουργία της συλλογής και της διάδοσης παρουσιάζονται στα σχήματα 7.13 και 7.14. Το σχήμα 7.13 δείχνει στα σταδιακά βήματα της λειτουργίας διάδοσης σε τοπολογία Γραμμής ενός παράλληλου συστήματος κατανεμημένης μνήμης. Το δεδομένο στέλνεται πρώτα από τον επεξεργαστή 0 στον επεξεργαστή 1. Ο επεξεργαστής 1 κρατάει ένα αντίγραφο για αυτόν και στέλνει ένα άλλο αντίγραφο στον επεξεργαστή 2. Η διαδικασία αυτή συνεχίζεται μέχρι το δεδομένο να φτάσει στον επεξεργαστή n στο δεξί άκρο της Γραμμής. Έστω ότι η καθυστέρηση της επικοινωνίας μεταξύ των γειτονικών επεξεργαστών είναι T και έστω ότι ο χρόνος υπολογισμού που απαιτείται από κάθε επεξεργαστή για την αντιγραφή του δεδομένου είναι αμελητέος σε σχέση με την καθυστέρηση της επικοινωνίας. Τότε ο συνολικός χρόνος εκτέλεσης για τη λειτουργία της διάδοσης σε μια τοπολογία Γραμμής με n+1 επεξεργαστές είναι nT.

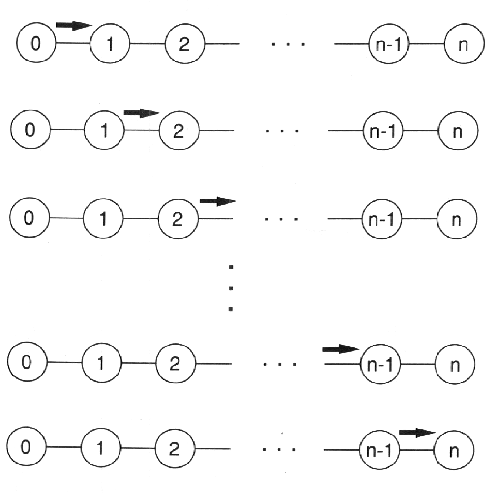
ΣΧΗΜΑ 7.13 Διάδοση σε τοπολογία γραμμής

Η λειτουργία της συλλογής παρουσιάζεται στο σχήμα 7.14. Κάθε επεξεργαστής έχει τη δική του τιμή δεδομένων. Έστω ότι αυτή η τιμή είναι τύπου Boolean και ότι η λειτουργία σύγκρισης είναι η λογική πράξη AND. Κατά τη διάρκεια του πρώτου βήματος ο επεξεργαστής n στέλνει την Boolean τιμή του στον επεξεργαστή n-1. Στην συνέχεια ο επεξεργαστής n-1 θα συγκρίνει την τιμή αυτή με την δική του τιμή εφαρμόζοντας την λογική πράξη AND. Την Boolean τιμή που θα προκύψει θα την στείλει ο επεξεργαστής n-1 στον γείτονα που βρίσκεται στα αριστερά του. Αυτή η επικοινωνία και η εφαρμογή της AND πραγματοποιούνται σε κάθε διαδοχικό επεξεργαστή, μέχρι να φτάσει το τελικό αποτέλεσμα στον επεξεργαστή 0. Αν υποθέσουμε ότι ο χρόνος εκτέλεσης και ο χρόνος που απαιτείται για την εφαρμογή της AND είναι αμελητέος σε σχέση με το χρόνο επικοινωνίας, τότε ο συνολικός χρόνος εκτέλεσης για τη λειτουργία της συλλογής είναι ακριβώς ίδιος με αυτόν της λειτουργίας διάδοσης, δηλαδή nT.

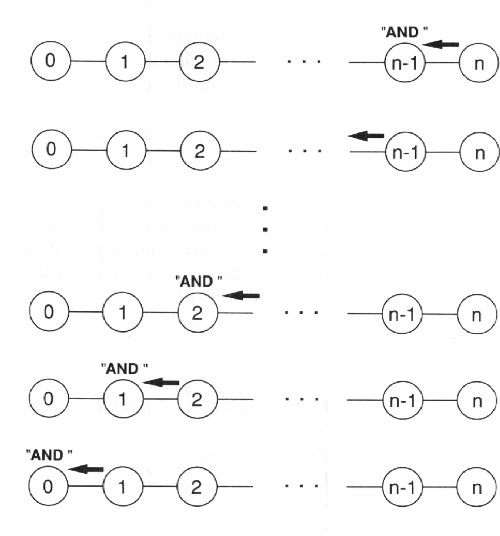
ΣΧΗΜΑ 7.14 Συλλογή σε τοπολογία γραμμής

Στην τοπολογία Δακτυλίου η λειτουργία της διάδοσης μπορεί να πραγματοποιηθεί στον μισό χρόνο, όπως φαίνεται στο σχήμα 7.15. Ο επεξεργαστής 0 στέλνει ένα αντίγραφο της τιμής δεδομένων και προς τις δυο κατευθύνσεις στον Δακτύλιο. Έτσι, το συνολικό πλήθος βημάτων επικοινωνίας που απαιτούνται για έναν Δακτύλιο με n επεξεργαστές είναι μόνο n/2. Και εδώ όπως και στην τοπολογία Γραμμής η λειτουργία της συλλογής είναι αντίθετη από αυτή της διάδοσης. Στο σχήμα 7.15 οι επεξεργαστές 4 και 5 αρχίζουν και οι δύο την λειτουργία της συλλογής στέλνοντας τις τιμές δεδομένων τους προς τους άμεσους γείτονες τους και προς την κατεύθυνση του επεξεργαστή 0. Και στις δύο πλευρές του Δακτυλίου γίνονται παράλληλοι υπολογισμοί και συνεπώς ο συνολικός χρόνος που απαιτείται είναι ο μισός σε σχέση με την τοπολογία Γραμμής.

Στην τοπολογία δι-διάστατου Πλέγματος η διάδοση γίνεται με την αποστολή των δεδομένων κατά μήκος της γραμμής που βρίσκεται στην κορυφή, στους επεξεργαστές δηλαδή που βρίσκονται στην κορυφή κάθε στήλης. Στη συνέχεια τα δεδομένα παράλληλα κινούνται κάθετα σε κάθε στήλη. Όλη αυτή η διαδικασία φαίνεται στο σχήμα 7.16. τα μαύρα βέλη πάνω στο σχήμα δείχνουν την κατεύθυνση προς την οποία κινούνται τα βέλη. Ο συνολικός χρόνος που απαιτείται για τη λειτουργία της διάδοσης είναι ανάλογος προς το μήκος του μονοπατιού από τον επεξεργαστή 0, που βρίσκεται στην άνω αριστερή γωνία του πλέγματος, προς τον επεξεργαστή που βρίσκεται στην κάτω δεξιά γωνία του πλέγματος. Σε ένα Πλέγμα διαστάσεων mxm το μήκος του μονοπατιού είναι 2(m-1), που είναι ακριβώς ίσο με τη διάμετρο του δικτύου. Αυτή η ίδια ιδιότητα ισχύει και στο χρόνο διάδοσης στο Δακτύλιο και στο Πλέγμα. Στις τοπολογίες Γραμμής, Δακτυλίου και δι-διάστατου Πλέγματος οι χρόνοι εκτέλεσης των λειτουργιών της διάδοσης και της συλλογής είναι απλά η διάμετρος της τοπολογίας επί την καθυστέρηση επικοινωνίας σε ένα σύνδεσμο. Από τον ορισμό της διαμέτρου είναι φανερό αυτό θα καθορίζει τον θεωρητικό ελάχιστο χρόνο που θα απαιτείται για τη διάδοση και την συλλογή. Για όλες τις τοπολογίες είναι δυνατόν να επιτευχθεί αυτός ο βέλτιστος χρόνος εκτέλεσης.

Στην λειτουργία της συλλογής στην τοπολογία του δι-διάστατου Πλέγματος μπορούμε απλώς να αντιστρέψουμε την κατεύθυνση από τα βέλη του σχήματος 7.16. Για μια τοπολογία Τόρου ιδίων διαστάσεων οι λειτουργίες της διάδοσης και τις συλλογής μπορούν να γίνουν στο μισό χρόνο. Η τεχνική που χρησιμοποιείται είναι

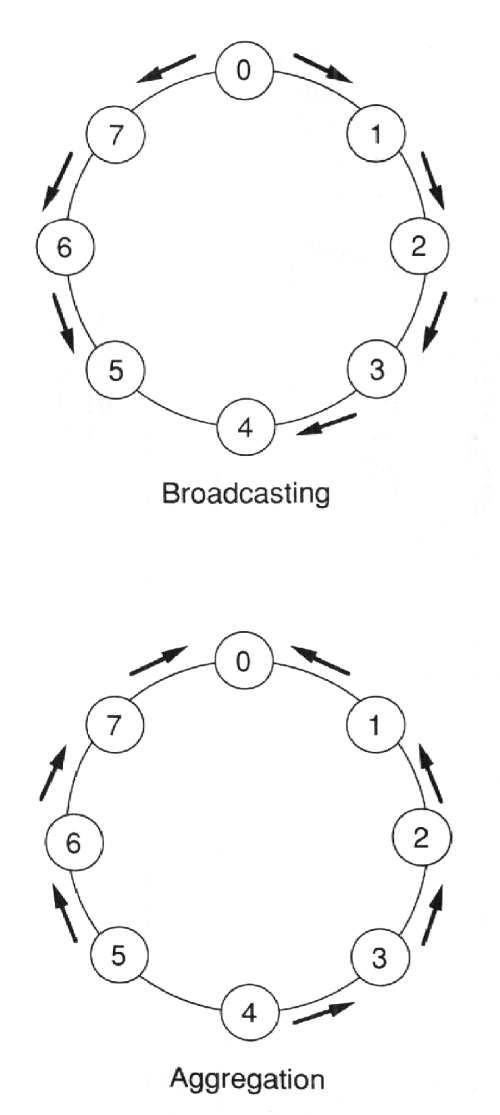
ΣΧΗΜΑ 7.15 Διάδοση και Συλλογή σε τοπολογία δακτυλίου

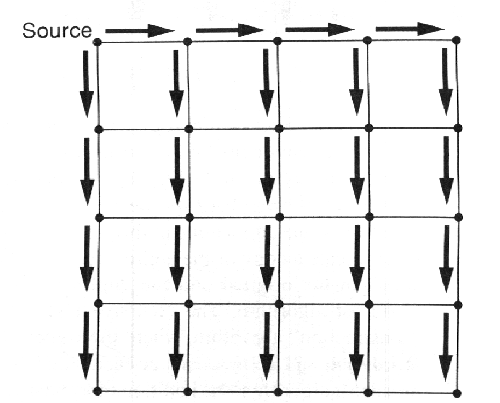
ΣΧΗΜΑ 7.16 Διάδοση σε δι-διάστατο πλέγμα

παρόμοια με αυτή του δι-διάστατου Πλέγματος: τα δεδομένα στέλνονται κατά μήκος της πρώτης γραμμής και στη συνέχεια διαδοχικά σε όλες τις στήλες. Σε ένα δι-διάστατο Πλέγμα κάθε στήλη ή κάθε γραμμή είναι μια δομή “Γραμμής”. Όμως, η πρόσθεση επιπλέον συνδέσεων μετατρέπει κάθε γραμμή και στήλη σε δομή “Δακτυλίου”. Έτσι, ο χρόνος που απαιτείται για την διάσχιση κάθε στήλης ή γραμμής είναι ο μισός σε σχέση με την Τοπολογία Τόρου χρησιμοποιώντας την τεχνική που έχουμε χρησιμοποιήσει στην τοπολογία Δακτυλίου (δες το σχήμα 7.15). Για έναν Τόρο mxm το πλήθος των βημάτων επικοινωνίας που απαιτούνται για την μετάδοση των δεδομένων κατά μήκος της πρώτης γραμμής είναι m/2 και το ίδιο ισχύει και για την στήλη. Αν η καθυστέρηση επικοινωνίας για έναν μόνο σύνδεσμο είναι T μονάδες χρόνου, τότε η συλλογή και η διάδοση σε έναν Τόρο απαιτούν Tm/2 χρόνο εκτέλεσης. Όπως και στην Γραμμή, το Δακτύλιο και το δι-διάστατο Πλέγμα αυτός ο T χρόνος πολλαπλασιάζεται με τη διάμετρο της τοπολογίας.

Στην τοπολογία τρισ-διάστατου Πλέγματος ο επεξεργαστής 0 στέλνει ένα αντίγραφο των δεδομένων στην άνω αριστερή γωνία κάθε επιπέδου. Στην συνέχεια η μετάδοση του αντίγραφου σε όλα τα επίπεδα γίνεται παράλληλα. Η διαδικασία που χρησιμοποιείται από κάθε επίπεδο είναι η ίδια με αυτή που χρησιμοποιείται και για το δι-διάστατο Πλέγμα, εφόσον κάθε επίπεδο είναι ένα δι-διάστατο Πλέγμα με κάποιες επιπλέον συνδέσεις. Για ένα 3x3x3 Πλέγμα η λειτουργία της διάδοσης φαίνεται στο σχήμα 7.17. Η λειτουργία περιλαμβάνει σημαντικό βαθμό παραλληλισμού, που μειώνει το συνολικό χρόνο εκτέλεσης κατά την κυβική ρίζα του πλήθους των επεξεργαστών. Για ένα mxmxm Πλέγμα η λειτουργία της διάδοσης έχει χρόνο εκτέλεσης 3T(m-1), ο χρόνος για τη συλλογή είναι ο ίδιος.

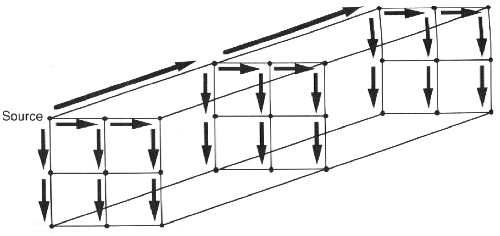
ΣΧΗΜΑ 7.17 Διάδοση σε τρισ-διάστατο πλέγμα

Σε μια τοπολογία Υπερκύβου με διάσταση d, ο θεωρητικά ελάχιστος χρόνος για τις λειτουργίες της διάδοσης και της συλλογής είναι Td. Για να επιτύχουμε αυτόν το χρόνο χρειαζόμαστε έναν αλγόριθμο που να βασίζεται στον αναδρομικό ορισμό της δομή του Υπερκύβου, όπως αυτός παρουσιάστηκε σε προηγούμενη παράγραφο. Αν ξαναδούμε το σχήμα 7.12 θα παρατηρήσουμε ότι η βάση του αναδρομικού ορισμού του Υπερκύβου είναι ο διπλασιασμός της προηγούμενης δομής σε κάθε στάδιο. Για να μετακινηθούμε από το στάδιο n στο n+1 δημιουργούμε ένα αντίγραφο όλης της δομής του σταδίου n και μετά συνδέουμε τα αντίστοιχα σημεία του προτύπου με το διπλασιασμένο. Αυτό μπορεί να χρησιμοποιηθεί ως βάση ενός αναδρομικού αλγορίθμου διάδοσης. Ο αναδρομικός ορισμός του Υπερκύβου μπορεί να θεωρηθεί σαν ένας αλγόριθμος κατασκευής, όπου ο Υπερκύβος στην ουσία κατασκευάζεται προσθέτοντας νέους επεξεργαστές και συνδέσεις σε κάθε στάδιο. Για να αλλάξουμε αυτόν τον αλγόριθμο κατασκευής σε έναν αλγόριθμο διάδοσης αντικαθιστούμε την πρόσθεση της σύνδεσης μεταξύ των αντίστοιχων επεξεργαστών του πρότυπου και του διπλασιασμένου με μια επικοινωνία μεταξύ του πρότυπου και των αντίστοιχων επεξεργαστών του διπλασιασμένου.

Τα διαδοχικά βήματα αυτού του αναδρομικού αλγόριθμου διάδοσης φαίνονται στο σχήμα 7.18. Στο βήμα 1 ο επεξεργαστής 0 στέλνει ένα αντίγραφο των δεδομένων στον επεξεργαστή 1. Στο επόμενο βήμα, οι επεξεργαστές 0 και 1 στέλνουν στους διπλασιασμένους αντίστοιχους επεξεργαστές τους. Κάθε επεξεργαστής μπορεί να βρει το αντίστοιχο αντίγραφό του προσθέτοντας ένα δυαδικό “1” στα αριστερά του δικού του αριθμού. Στο βήμα 3, καθένας από τους τέσσερις επεξεργαστές που τώρα έχουν ένα αντίγραφο των δεδομένων, στέλνουν ένα αντίγραφο στους διπλασιασμένους τους, που επιλέγονται πάλι προσθέτοντας ένα “1” στα αριστερά του αριθμού τους (δες σχήμα 7.18). Και οι τέσσερις αυτές επικοινωνίες του βήματος 3 συμβαίνουν παράλληλα. Στο βήμα 4 κάθε επεξεργαστής που έχει ένα αντίγραφο των δεδομένων στέλνει ένα άλλο αντίγραφο στο αντίστοιχο αντίγραφό του, που επιλέγεται με την ίδια μέθοδο. Αν ο Υπερκύβος έχει διάσταση d είναι φανερό ότι αυτός ο αναδρομικός αλγόριθμος θα απαιτήσει d βήματα για να φτάσει όλους τους επεξεργαστές του Υπερκύβου.

Εφόσον ο Υπερκύβος έχει διάσταση d, υπάρχουν συνολικά d θέσεις bits στον αριθμό του κάθε επεξεργαστή. Αυτές οι θέσεις bits μπορούν να αριθμηθούν από τα δεξιά προς τα αριστερά. Από τον αναδρομικό αλγόριθμο διάδοσης που φαίνεται

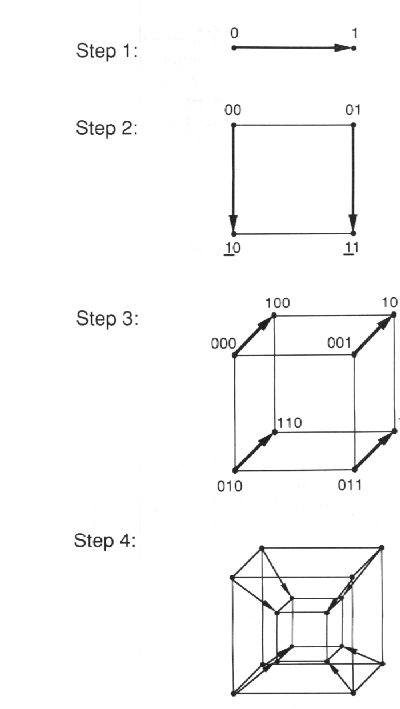
ΣΧΗΜΑ 7.18 Διάδοση σε υπερκύβο

στο σχήμα 7.18 είναι φανερό ότι οι επεξεργαστές που μπλέκονται στην επικοινωνία κατά τη διάρκεια του βήματος i είναι αυτοί που των οποίων ο αριθμός έχει 0 στις bit θέσεις από i+1 ως d. Από τους επεξεργαστές που επικοινωνούν κατά τη διάρκεια του βήματος i αυτοί που έχουν 0 στη θέση i είναι οι αποστολείς και αυτοί που έχουν 1 στην ίδια θέση είναι οι παραλήπτες. Είναι δυνατόν να γράψουμε μια απλή επαναληπτική διαδικασία που να πραγματοποιεί την λειτουργία της διάδοσης. Αυτό γίνεται σε μια από τις ασκήσεις στο τέλος του κεφαλαίου.

Όπως σε όλες τις προηγούμενες τοπολογίες, ο αλγόριθμος συλλογής μπορεί να οριστεί απλώς με την ανάλυση της διάδοσης αντίστροφα στο χρόνο και αντιστρέφοντας τις κατευθύνσεις όλων των επικοινωνιών. Για έναν Υπερκύβο με n επεξεργαστές οι αλγόριθμοι συλλογής και διάδοσης έχουν ίδιο χρόνο εκτέλεσης που είναι O(logn), που είναι και η διάσταση του Υπερκύβου. Είναι ενδιαφέρον να αναφέρουμε ότι αυτοί οι αλγόριθμοι που παρουσιάζονται στο σχήμα 7.18 είναι παρόμοιοι με τον αλγόριθμο τουρνουά που παρουσιάστηκε στο κεφάλαιο 6. Ο αλγόριθμος τουρνουά πραγματοποιεί συλλογή και διάδοση που απαιτούν O(logn) χρόνο. Η μέθοδος τουρνουά μπορεί επίσης να εφαρμοστεί στην πραγματοποίηση μιας συλλογής ή μιας διάδοσης σε έναν Υπερκύβο. Κάτι τέτοιο ζητείται από τις ασκήσεις αυτού του κεφαλαίου. Το ακόλουθο σχεδιάγραμμα αποτελεί περίληψη του χρόνου εκτέλεσης που απαιτείται για διάδοση ή για συλλογή για καθεμία από τις τοπολογίες και για n επεξεργαστές:

Τοπολογία Χρόνος Διάδοσης

Γραμμή O(n)

Δακτύλιος O(n)

2-D Πλέγμα O(n^1/2)

Τόρος O(n^1/2)

3-D Πλέγμα O(n^1/3)

Υπερκύβος O(logn)